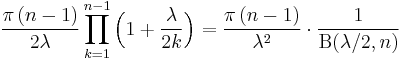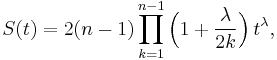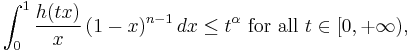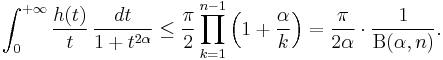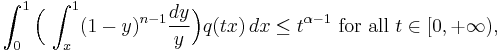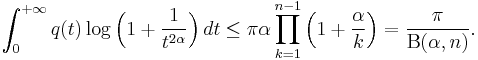Khabibullin's conjecture on integral inequalities

In mathematics, Khabibullin's conjecture, named after B. N. Khabibullin, is related to Paley's problem[1] for plurisubharmonic functions and to various extremal problems in the theory of entire functions of several variables.

Contents

The first statement in terms of logarithmically convex functions

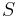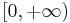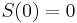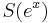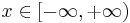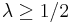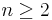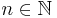Khabibullin's conjecture (version 1, 1992). Let \displaystyle S be a non-negative increasing function on the half-line [0,%2B\infty) such that \displaystyle S(0)=0. Assume that \displaystyle S(e^x) is a convex function of x\in[-\infty,%2B\infty). Let \lambda\geq 1/2, n\geq 2, and n\in\mathbb N. If

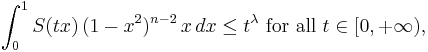
\int^1_0 S(tx)\,(1-x^2)^{n-2}\,x\,dx\leq t^\lambda\text{ for all }t\in[0,%2B\infty),

 

 

 

 

(1)

then

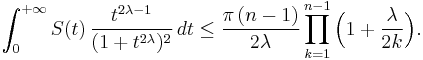
\int^{%2B\infty}_0 S(t)\,\frac{t^{2\lambda-1}}{(1%2Bt^{2\lambda})^2}\,dt\leq \frac{\pi\,(n-1)}{2\lambda}\prod_{k=1}^{n-1} \Bigl(1%2B\frac{\lambda}{2k}\Bigr).

 

 

 

 

(2)

This statement of the Khabibullin's conjecture completes his survey.[2]

Relation to Euler's Beta function

Note that the product in the right hand side of the inequality (2) is related to the Euler's Beta function 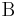\Beta:

\frac{\pi\,(n-1)}{2\lambda}\prod_{k=1}^{n-1} \Bigl(1%2B\frac{\lambda}{2k}\Bigr)=\frac{\pi\,(n-1)}{\lambda^2}\cdot\frac{1}{\Beta(\lambda/2,n)}

Discussion

For each fixed 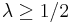\lambda\geq 1/2 the function

S(t)=2(n-1)\prod_{k=1}^{n-1} \Bigl(1%2B\frac{\lambda}{2k}\Bigr) \, t^{\lambda},

turns the inequalities (1) and (2) to equalities.

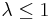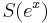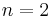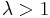The Khabibullin's conjecture is valid for \lambda\leq 1 without the assumption of convexity of S(e^x). Meanwhile, one can show that this conjecture is not valid without some convexity conditions for S. Nowadays it is even unknown if the conjecture is true for n=2 and for at least one \lambda>1.

The second statement in terms of increasing functions

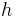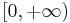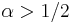Khabibullin's conjecture (version 2). Let \displaystyle h be a non-negative increasing function on the half-line [0,%2B\infty) and \alpha>1/2. If

\int_0^1 \frac{h(tx)}{x} \,(1-x)^{n-1}\,dx \leq t^\alpha\text{ for all }t\in[0,%2B\infty),

then

\int_0^{%2B\infty}\frac{h(t)}{t}\,\frac{dt}{1%2Bt^{2\alpha}}\leq \frac{\pi}{2} \prod_{k=1}^{n-1} \Bigl(1%2B\frac{\alpha}{k}\Bigr)= \frac{\pi}{2\alpha} \cdot \frac{1}{\mathrm B (\alpha, n)}.\,

The third statement in terms of non-negative functions

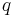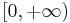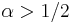Khabibullin's conjecture (version 3). Let \displaystyle q be a non-negative continuous function on the half-line [0,%2B\infty) and \alpha>1/2. If

\int_0^1 \Bigl(\,\int_x^1 (1-y)^{n-1} \frac{dy}{y}\Bigr)q(tx)\,dx \leq t^{\alpha-1}\text{ for all }t\in[0,%2B\infty),

then

\int_0^{%2B\infty} q(t)\log \Bigl(1%2B\frac1{t^{2\alpha}}\Bigr)\,dt\leq \pi \alpha \prod_{k=1}^{n-1} \Bigl(1%2B\frac{\alpha}{k}\Bigr)= \frac{\pi}{\mathrm B (\alpha, n)}.\,

References

  1. ^ Khabibullin B.N. (1999). "Paley problem for plurisubharmonic functions of finite lower order". Sbornik: Mathematics 190 (2): 309–321. 
  2. ^ Khabibullin BN (2002). "The representation of a meromorphic function as the quotient of entire functions and Paley problem in 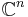\displaystyle\mathbb C^n: a survey of some results". Mat. Fizika, analiz, geometria 9 (2): 146–167. arXiv:math.CV/0502433.